Ранее у нас была заметка про Origin у PlanarFace, где мы писали, что Origin может не находиться в границах контура плоскости PlanarFace. А недавно мы столкнулись с еще одной недокументированной особенностью Revit API, которая в некоторых случаях может привести к неправильной работе задуманного алгоритма. И эта особенность – свойство Origin у отрезка, полученного методом Solid.IntersectWithCurve.
Опишем сразу на примере: создадим в пустом проекте элемент с твердым телом и возьмём его твердое тело:
var uiDoc = commandData.Application.ActiveUIDocument;
var doc = uiDoc.Document;
var element = doc.GetElement(uiDoc.Selection.PickObject(ObjectType.Element));
var solid = (Solid)element
.get_Geometry(new Options { DetailLevel = ViewDetailLevel.Fine })
.GetTransformed(Transform.Identity)
.First(e => e is Solid { Volume: > 0 });
Так как для примера мы использовали колонну, то мы точно знаем, что у неё есть точка вставки. Возьмем эту точку и с ее помощью создадим длинный вспомогательный отрезок:
var pt = ((LocationPoint)element.Location).Point;
var helpLine = Line.CreateBound(
pt - (XYZ.BasisZ * 1000),
pt + (XYZ.BasisZ * 1000));
Ну а далее используем метод Solid.IntersectWithCurve и получим отрезок, расположенный внутри твердого тела нашего элемента:
var result = solid.IntersectWithCurve(
helpLine,
new SolidCurveIntersectionOptions { ResultType = SolidCurveIntersectionMode.CurveSegmentsInside });
var insideLine = (Line)result.GetCurveSegment(0);
Так вот, если теперь мы посмотрим на свойства этого отрезка, то увидим, что его Origin остался такой-же, как был у исходного вспомогательного отрезка! И если вы возьмете у этого отрезка параметры в начале и в конце, то получите не самые ожидаемые значения:
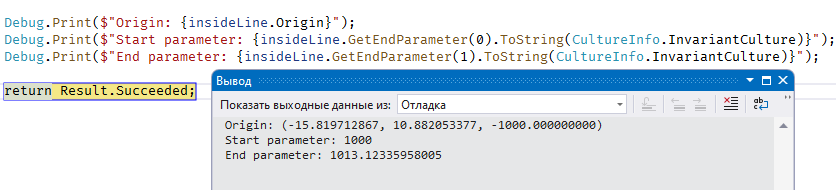
И хотя случаев, где это может негативно сказаться на работе алгоритма, не много, они все же есть. Поэтому лучше знать про эту особенность заранее
Comments
Столкнулся сегодня с задачей, в которой мне необходимо было высчитать производные в точке для дуги. Как и прежде я снова открыл справку и, так как я не обладаю высшим геометрическим образованием, я снова впал в ступор с вопросом «Какое же значение мне нужно?». Поэтому я решил сделать для себя и для всех небольшую шпаргалку-визуализацию.
Суть шпаргалки – получить визуальное представление для векторов класса Transform, получаемых при использовании метода Curve.ComputeDerivatives
Comments
Подробнее: Revit. Визуализация ComputeDerivatives для Line и Arc
Как оказалось, в Revit API нет методов, позволяющих разделить кривую Curve на части заданной длины. Именно такая задача недавно у меня при разработке плагина. В AutoCAD API есть хороший метод GetPointAtDist, который позволяет решить данную задачу, но в Revit API пришлось решать её самому.
В моем случае мне нужно было получить точки деления кривой на части заданной длины. Для решения задачи нам понадобятся параметры кривой. Получаем начальный и конечный параметр и через интерполяцию находим шаг параметризации, равнозначный длине части. Далее просто делаем цикл, прибавляя шаг параметризации, до тех пор, пока сумма шагов не достигнет конечного параметра. Если шаг по длине не делит кривую на равнозначные части (в конце остается участок меньшей длины, чем заданная длина части), берем ещё конечную точку. Если заданная длина части вдруг оказалась меньше длины кривой, берем конечные точки:
/// <summary>
/// Возвращает точки деления кривой на части указанной длины
/// </summary>
/// <param name="curve">Кривая</param>
/// <param name="step">Шаг деления</param>
public static IEnumerable<XYZ> Divide(this Curve curve, double step)
{
if (curve.Length > step)
{
var startParameter = curve.GetEndParameter(0);
var endParameter = curve.GetEndParameter(1);
var parameterStep = (endParameter - startParameter) / (curve.Length / step);
var parameterSum = startParameter;
do
{
yield return curve.Evaluate(parameterSum, false);
parameterSum += parameterStep;
}
while (parameterSum < endParameter);
if (Math.Abs(parameterSum - endParameter) > 0.0001)
yield return curve.GetEndPoint(1);
}
else
{
yield return curve.GetEndPoint(0);
yield return curve.GetEndPoint(1);
}
}
Данную идею можно реализовать и для других схожих задач: взять точку на определенном расстоянии, поделить кривою на заданное количество частей и т.д. Главное, что нужно понять из данной записи – все подобные задачи необходимо решать через параметры кривой.
Comments
Стояла у меня задача, для выполнения которой требовалось создание собственного типа для системного семейства Текст (Текстовое примечание).
Немного поискав информацию на просторах интернета, я наткнулся на данный пример, объясняющий, что для создания типа требуется создавать дубликат существующего типа. Вот только в примере совсем не уделено внимание тому, как и какие параметры задавать. Особенно остро стоит вопрос задания значения для параметра «Цвет».
Почитав в теме комментарии, я понял, что вопрос волновал многих и, к моему сожалению, в комментариях нет правильного ответа. Я решил исправить эту маленькую несправедливость и сделал небольшой пример создания типа для системного семейства Текст. Все пояснения я оставил в виде комментариев к коду.
Вот и сам пример:
Comments
Подробнее: Создание типа для системного семейства Текст (TextNoteType)





